JOISC 2018 D 修行 (Asceticism)

標籤： joimath

题意

给定 $n$ 和 $k$，求有多少个 1-n 的排列 $p$ 使得恰好存在 $k$ 个不同的位置 $i$ 满足 $p_{i} > p_{i+1}$。

即是 Eulerian Number 单点求值。

• $1 \le k+1 \le n \le 1 \times 10^5$

解析

求一个这种排列的数量可以转化为求出现概率。而某种长度为 $n$ 的排列的出现概率其实是可以转化为有 $n$ 个取值为 $[0, 1)$ 的连续随机变量的，为两个连续随机变量相等的概率为 0，排列中两个值相等的概率也是 0，每一组随机变量的偏序关系都可以对应成一个排列。

要求刚好有 $k$ 个满足 $p_{i} > p_{i+1}$ 的不好解决，考虑求至多有 $k$ 个，即令 $f(k)$ 表示小于有 $k$ 个位置满足 $p_{i} > p_{i+1}$ 的概率，要求的答案就是 $f(k+1)-f(k)$。

假设我们随机的序列叫作 $a_{1}, a_{2}, \cdots, a_{n}$，令：

$$b_{i}= \begin{cases} a_{1} & i=1 \\ a_{i}-a_{i-1} + [a_{i} < a_{i-1}] & i>1 \end{cases}$$

这个 $b$ 与 $a$ 是一一对应的，可以想象成有一个环，则这个 $b_{i}$ 就是在环上 $a_{i-1}$ 到 $a_{i}$ 的步长。同时，$b$ 的值域和 $a$ 一样，都是 $[0, 1)$。容易发现，如果 $a$ 有不超过 $k$ 个位置满足那个条件，则有 $\sum b < k+1$。换句话说，我们要求的就是 $f(k)$ 就是找 $\sum b < k$ 的概率。

如何求 $\sum b < k$ 的概率呢？参考某一道叫作 Hyperrectangle 的题目。考虑一个 $n$ 维坐标系，这个问题就转化为，有一个超立方体，从 $(0,0,\cdots,0)$ 到 $(1,1,\cdots,1)$，与一个 $\sum_{i=1}^{n} x_{i} = k$ 的超平面，问这个超立方体被这个超平面切割后的体积与原体积（即 1）之比。如图：

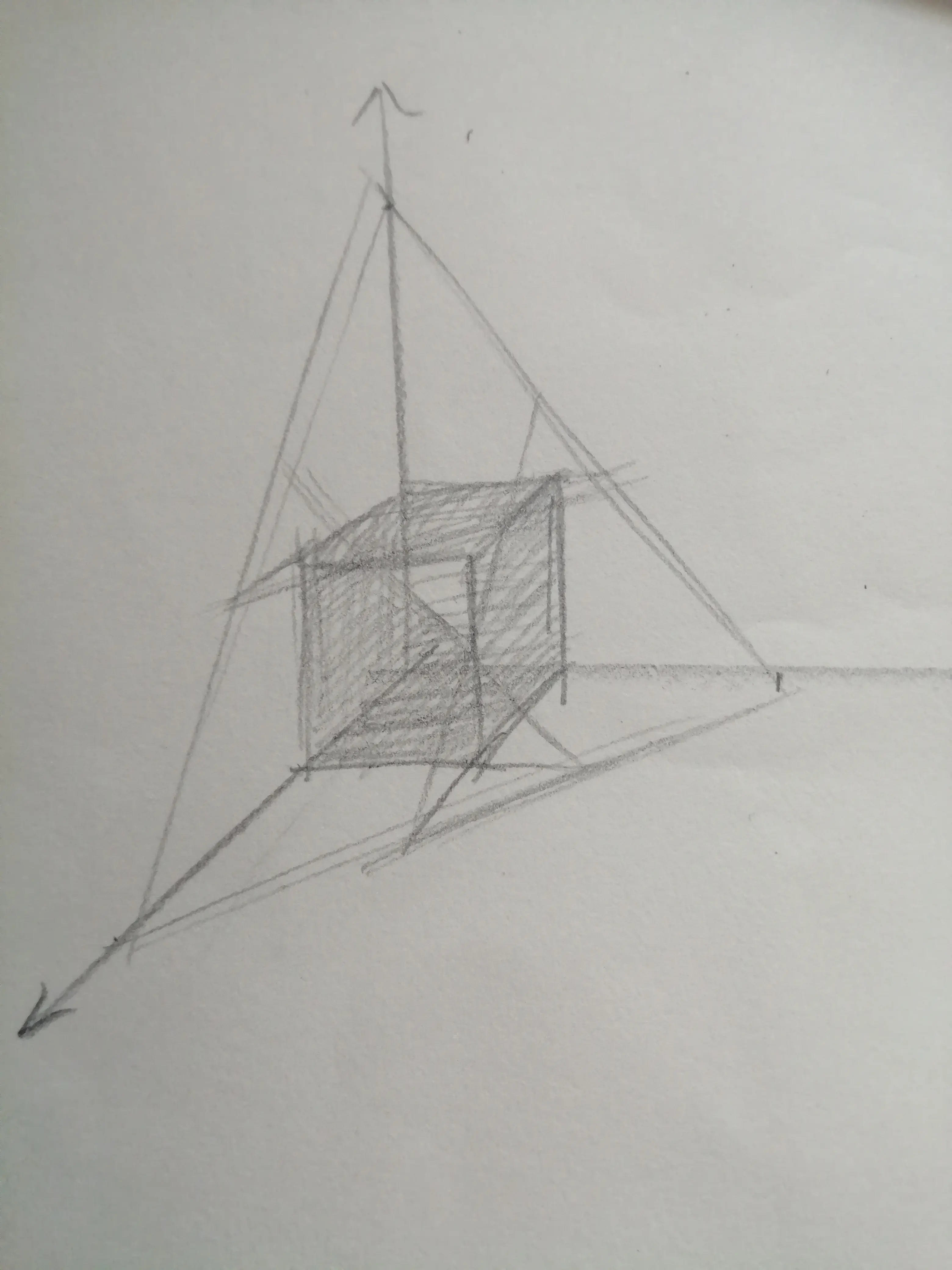
接下来考虑求这个被切割的体积。首先考虑没有这个超立方体的限制，令 $S_{n}(k)$ 表示在 $n$ 维中 $\sum_{i=1}^{n} x_{i} < k\ (x_{i}\ge 0)$ 的体积。

• 当 $n=2$ 时，是三角形，容易得到 $S_{2}(k)=\frac{k^2}{2}$。
• 当 $n=3$ 时，是棱锥，容易得到 $S_{3}(k)=\frac{k^3}{6}$。
• 猜测 $S_{n}(k)=\frac{k^n}{n!}$。通过数学归纳法：

$$\begin{aligned} S_{n}(k) &= \int_{0}^{k} S_{n-1}(x) \mathrm{d}x \\ &= \int_{0}^{k} \frac{x^{n-1}}{(n-1)!} \mathrm{d}x \\ &= \frac{1}{(n-1)!} \cdot \int_{0}^{k} x^{n-1} \mathrm{d}x \\ &= \frac{1}{(n-1)!} \cdot \frac{k^n}{n} \\ &= \frac{k^n}{n!} \end{aligned}$$

当然还有一种比较感性的理解方法。我们要求 $n$ 维中 $\sum_{i=1}^{n} x_{i} < k\ (x_{i}\ge 0)$ 的体积。令 $y_{i} = \sum_{j=1}^{i} x_{j}$，即 $x$ 的前缀和，$y$ 和 $x$ 是一一对应的。由于和不超过 $k$，所以 $y_{i}$ 可以取 $[0, k)$ 的所有值，体积为 $k^n$。同时，由于 $x_{i} \ge 0$，故 $y_{i}$ 是单调递增的，所以需要再除以 $n!$，即 $\frac{k^n}{n!}$。

然后对于这个超立方体的限制，可以容斥。令 $g(t)$ 表示有 $t$ 个坐标在 $[1, k)$ 中， $n-t$ 个坐标在 $[0, k)$ 中，满足 $\sum x < k$ 的体积。实际上，加上这个限制可以当作有 $t$ 个坐标轴平移了 1 个单位，可以得到 $g(t)=S_{n}(k-t)$。所以总的体积（概率）就是：

$$\begin{aligned} f(k) &= \sum_{i=0}^{k} (-1)^i \cdot \binom{n}{i} \cdot g(i) \\ &= \sum_{i=0}^{k} (-1)^i \cdot \binom{n}{i} \cdot \frac{(k-i)^n}{n!} \end{aligned}$$

时间复杂度 $O(n\log n)$，这个 $\log$ 是快速幂。

实现

#include <iostream>
#include <vector>
#include <algorithm>

const int M = 1'000'000'007;

int pow_mod(int x, int y)
{
	int r = 1;
	while (y) {
		if (y & 1) r = (long long)r * x % M;
		x = (long long)x * x % M;
		y >>= 1;
	}
	return r;
}

int get_inv(int x)
{
	return pow_mod(x, M - 2);
}

int main()
{
	int n, k;
	std::cin >> n >> k;

	std::vector<int> fac(n * 2 + 1), ifac(n * 2 + 1);
	fac[0] = 1;
	for (int i = 1; i <= n * 2; i++) fac[i] = (long long)fac[i - 1] * i % M;
	ifac.back() = get_inv(fac.back());
	for (int i = n * 2; i > 0; i--) ifac[i - 1] = (long long)ifac[i] * i % M;
	auto binom = [&fac, &ifac](int n, int m)
	{
		return (long long)fac[n] * ifac[m] % M * ifac[n - m] % M;
	};

	auto f = [&fac, &ifac, &binom](int n, int k)
	{
		int res = 0;
		for (int i = 0; i <= k; i++) {
			int t = (long long)pow_mod(k - i, n) * ifac[n] % M * binom(n, i) % M;
			if (i % 2 == 1) res = (res + M - t) % M;
			else res = (res + t) % M;
		}
		return res;
	};

	k--;
	int p = (f(n, k + 1) + M - f(n, k)) % M;
	std::cout << (long long)p * fac[n] % M << std::endl;
}