CF 1815B Sum Graph

標籤： cfinteractiveconstructive

题意

交互题：有一个长度为 $n$ 的排列 $p$，和一个 $n$ 个节点 $0$ 条边的无向图。有两种询问：

1. 给定一个 $x$，对于所有的 $i$ $(1 \le i \le n)$ 使得 $1 \le x - i \le n$，在 $i$ 和 $x - i$ 间加一条边；
2. 询问 $p_i$ 和 $p_j$ 的最短路长度。

最多询问 $2n$ 次，求原排列。最多猜测两次。

解析

如果能把图连成一条链的话会比较好做。使用 + n 和 + (n+1) 两次加边操作把图连成这样的链：

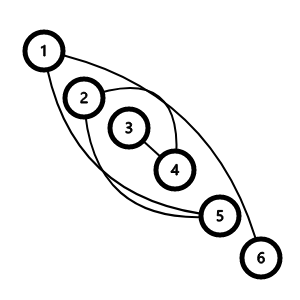
首先任意选取一个点 $s$，询问 $s$ 和其他所有点的距离，最远的那个节点 $t$ 就是链的某个端点。然后又询问 $t$ 和所有其他点的距离，就可以确定排列了。注意到链有两个端点，所以你会得到两个排列。

void solve() 
{
	int n;
	std::cin >> n;
	
	int successful;
	std::cout << "+ " << n << std::endl;
	std::cin >> successful;
	assert(successful == 1);
	std::cout << "+ " << n + 1 << std::endl;
	std::cin >> successful;
	assert(successful == 1);
	
	std::vector<int> dis0(n);
	dis0[0] = 0;
	for (int i = 1; i < n; i++) {
		std::cout << "? " << 1 << " " << i + 1 << std::endl;
		std::cin >> dis0[i];
	}
	
	int end = std::max_element(dis0.begin(), dis0.end()) - dis0.begin();
	std::vector<int> dis_end(n);
	dis_end[end] = 0;
	for (int i = 0; i < n; i++) {
		if (i == end) continue;
		std::cout << "? " << end + 1 << " " << i + 1 << std::endl;
		std::cin >> dis_end[i];
	}
	
	std::vector<int> p(n);
	std::iota(p.begin(), p.end(), 0);
	std::sort(p.begin(), p.end(), [&dis_end](int a, int b)
		  {
			  return dis_end[a] < dis_end[b];
		  });
	
	{
		std::vector<int> ans(n);
		for (int i = 0, j = n, t = 0; i < j && t < n;) {
			if (t < n) ans[p[t++]] = --j;
			if (t < n) ans[p[t++]] = i++;
		}
		std::cout << "! ";
		for (int i = 0; i < n; i++) {
			std::cout << ans[i] + 1 << " ";
		}
	}
	{
		std::vector<int> ans(n);
		for (int i = 0, j = n, t = n; i < j && t > 0;) {
			if (t > 0) ans[p[--t]] = --j;
			if (t > 0) ans[p[--t]] = i++;
		}
		for (int i = 0; i < n; i++) {
			std::cout << ans[i] + 1 << " ";
		}
		std::cout << std::endl;
	}
	
	std::cin >> successful;
	assert(successful);
}