AtCoder ABC 292 F Regular Triangle Inside a Rectangle

標籤： atmath

给定一个 $a \times b$ 的矩形，求能放在矩形中最大的正三角形。

首先我们先假定 $a \le b$。我们假设答案三角形有至少一个顶点和长方形某个顶点重合。因为对于任意一个正三角形，每个角都是 $\frac{\pi}{3}$，必然存在一个顶点使得它是最左上/左下/右上/右下角，可以把这个角对齐到长方形的某一个顶点上。除了这个点，至少还有一个点在长方形的边上（除了那个和长方形端点对齐的点），否则答案可以更优。

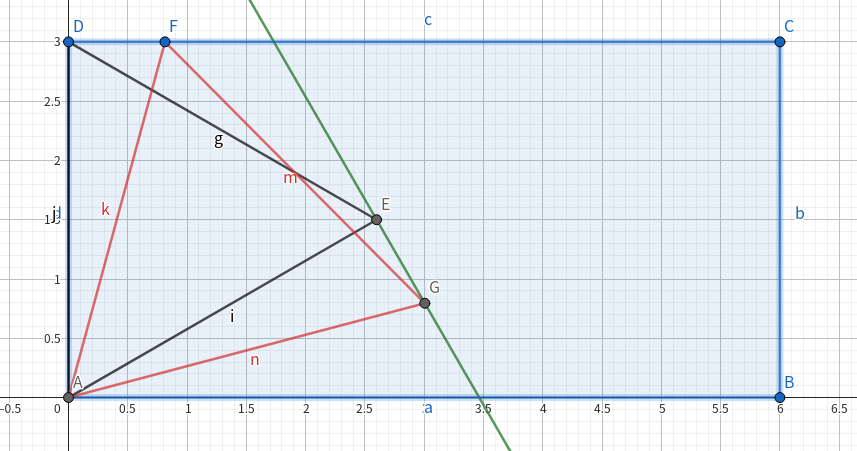
如图，$\triangle AFG$ 是我们要求的答案三角形。$A$ 是和长方形对齐的角， $F$ 是在 $DC$ 上运动的点。$\triangle ADE$ 也是正三角形，可以证得 $\triangle ADF$ 和 $\triangle AEG$ 全等，$E$ 又是顶点，$\angle AEG = \frac{\pi}{2}$，所以 $G$ 在如图的绿色直线上移动。$G$ 必须在长方形内，所以当 $G$ 处在 $AB$ 上或 $BC$ 上时答案最优。

具体来说，当 $b \ge a \sec \frac{\pi}{6}$ 时，$G$ 在 $AB$ 上，答案为 $a \sec \frac{\pi}{6}$，否则，$G$ 在 $BC$ 上，答案为 $\sqrt{b^2 + \left[\left(a \sec \frac{\pi}{6} - b\right) \tan \frac{\pi}{3}\right]^2}$

#define _USE_MATH_DEFINES

#include <cmath>
#include <iomanip>
#include <iostream>

int main()
{
	double a, b;
	std::cin >> a >> b;
	if (a > b) std::swap(a, b);

	std::cout << std::fixed << std::setprecision(15);

	auto maxl = a / std::cos(M_PI / 6);
	if (maxl < b) {
		std::cout << maxl << std::endl;
		return 0;
	}
	auto h = (maxl - b) * std::tan(M_PI / 3);
	std::cout << std::sqrt(b * b + h * h) << std::endl;
}

注意：使用 <cmath> 中的数学常数需要 _USE_MATH_DEFINES 宏。

推荐看看小日本的题解：F - Regular Triangle Inside a Rectangle 解説